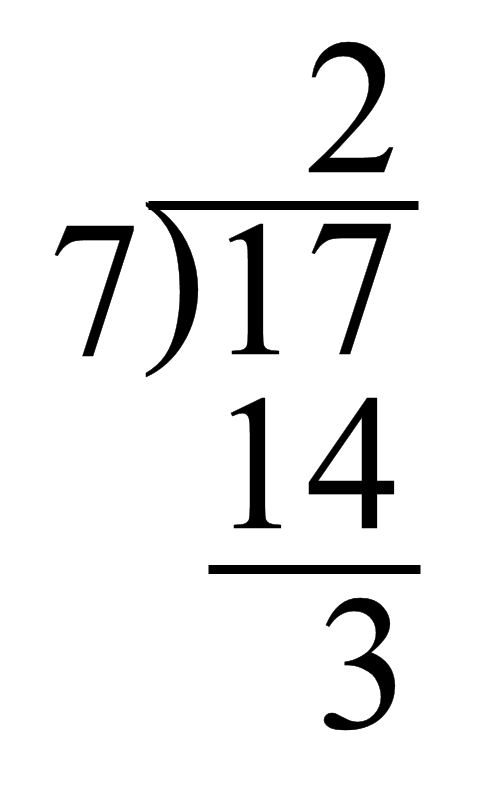Archive for the ‘Claude Monet’ Category
Entry 1078 — An Analysis of a Mathexpressive Poem
Friday, April 19th, 2013
A few people have told me (I don’t know how seriously) that they have not been able to figure out all the pieces I have in my latest entry in my Scientific American blog, and a few of mine colleagues even claim I can’t multiply. Ergo, I have an excuse to blither about one of my poems. I’ve chosen one I think the easiest to defend. First, though, here’s Monet’s The Regatta at Argenteuil. It’s important for one trying to understand my poem to know of it because it is central to the poem (as the third poem in my triptych makes clear with a full reproduction of it).
Okay, to begin with the simplicities of the poem below, a person encountering it must be aware that it is a long division example. That is indicated by two symbols: the one with the word, “poem,” inside it, and the line under the sailboat. The first, so far as I’m aware, has no formal name, so I call it a dividend shed. The line is a remainder line. The two together, along with the placement of the other elements of the poem, one where a long division’s quotient would be, one where its divisor would be, one where the product of the two would be, and one under the remainder line where a remainder would be, clinch the poem’s definition as long division.

Now, then, anyone remembering his long division from grade school, should understand that the poem is claiming five things:
(1) that the text the painter who is unsleeping a day long ago multiplied times the scribbled sketch, or whatever it is to the left of the dividend shed equals the sailboat shown;
(2) that the sailboat is larger in value that either the painter or the sketch;
(3) that the addition of the letter fragments under the remainder line to the sailboat image makes the sailboat equal the poem referred to above it;
(4) that the the sailboat should be considered almost equal to the poem;
(5) that the letter fragments, or whatever it is that they represent must be less in value than any of the other elements of the poem with the possible exception of the quotient.
(2) and (5) are decidedly less important than the other three, but can still be important.
I could easily claim that the poem is wholly accurate mathematically by giving the painter a value of 2, the sketch a value of 7, the sailboat a value of 14, the fragmented letters a value of 3 and the poem a value of 17. Arbitrary? Sure–but by definition as Grummanomical values of the elements mathematically correct however silly. (And I would contend that if I had time, I could given them Grummanomical poetic values most people would find acceptable, and–in fact–I believe one of the virtues of such a poem is that it will compel some to consider such things–at least to the extent of wondering how much value to give a painter’s activity, how much to a sketch, and whether a poem is genuinely better than either, or the like.)
I am including the above in my entry to help those a little fuzzy about long division (and I was definitely not unfuzzy about it when I began making long division poems, and still sometimes have to stop and think for more than a few minutes at times to figure out just what one of my creations is doing). My poem imitates it in every respect except that it does what it does with non-numerical terms rather than with numbers. I hope, however, that someone encountering it without knowing much or anything about such poems will at least find things to like in it such as the little poem about the painter, or the idea of the childish sketch as perhaps the basis of what would become a Grand Painting. Some, I believe, would enjoy recognizing the sailboat as the one in Monet’s masterpiece, too. But what is most important aesthetically about the work is what it does as a mathematical operation. That operation must make poetic sense if the work is to be effective. Needles to say, I claim it does.
To consider the question, we must break down the long division operation the poem depicts into its components. First of all, there is the multiplication of the sketch by what the painter is doing to get the sailboat–the painting of the sailboat, that is, sketch times something done by a painter almost having to yield a picture of some sort. Does this make sense? Clearly, a painter must carry out an operation on some initial sketch or idea or equivalent thereof to get into a painting, so I don’t see how one can wholly reject painter operating on sketch yields portion of painting as analogous to . . . 2 operating on 7 to yield 14. But there is more to it than that, if only to those of us who think of multiplication as magic, and are still in touch with the way we felt when the idea that 2 times 7 could make 14 was new to us. That is, just after we had internalized the remarkable mechanism for carrying out multiplication. For us, the poem’s painter is using his painting mechanism to hugely enlarge a sketch the way the operation of multiplication (usually) hugely enlarges a number. Doing so in a kind of concealed magical way unlike mere addition does. A three-dimensional way.
At this point, the question arises as to whether the sailboat nearly equal to a poem. That’s obviously a subjective matter. Those who like sailboats (and poems) will tend to say yes. Note, by the way, that “poem” here does not mean what I say it mean verosophically, but as what one of my dictionaries has it: “something suggesting a poem.” Here the context–a work of art–makes it impossible to take the word literally,–and moreover, of taking it to mean not just something suggesting a poem, but something suggestion a master-poem.
Well, not quite here: the penciled informality of the word, “poem,” counters the idea that a super-poem is being referred to, and the sailboat is only a black and white portion of a great painting, not a great painting by itself. We know it’s on its way to being that, but the multiplication is only telling us of it as a pleasant step, not anywhere close to being a realized goal.
The remainder, fragmented words, add very little to it, but we will later see that they are fragments of the phrase, “the faint sound of the unarrestable steps of Time.” Again, it’s a subjective matter as to whether these words could deepen anything sufficiently to enable it to suggest a poem. I say it does. But even if not, I think it would be hard to claim that the addition of such words to a visual image could not be called a plausible attempt to mathematically increase the image’s value.
In conclusion, I claim that the poem carries out the operation of long division in two steps, one multiplicative, the other additive, to valuable aesthetic effect. Elsewhere I have shown how, according to my thinking, it will put someone one appreciative of it into a Manywhere-at-Once partly in the verbal section of his brain and partly in the mathematical section of it. The next poem in the triptych goes somewhat further; the sequence’s final poem brings everything to a climax–I hope.
.
Entry 931 — Continuing the Monet Sequence
Friday, November 23rd, 2012
Finally into my creative-flow zone this morning after thinking I never again would be, I produced the following, which is the fourth frame in a sequence devoted to Monet I hope to continue:
Here’s the frame just before the above one, to provide context:
I’ve had it here before, I’m pretty sure, but if you look carefully, you’ll see a few small changes I’ve made to it since then. I still think it’s stupendously fine. Urp.
.