Entry 567 — Multiplication & Long Division
What follows is a piece it took me practically a week to get done, if it is indeed now done. It’s the first lesson hand-out for my exhibition.
THE JOY OF MULTIPLICATION AND LONG DIVISION
Multiplication is the best of the arithmetical procedures we learned in grade school for use in poetry because of something you might not expect of it: its richness. Consider something as simple as the poetic idea that “sunlight + soil = flowers.” Add sunlight to soil and you get flowers. (Well, you need more than that in real life, but not in poetry!) A nice enough idea that makes a pleasant poem because it expresses an old idea in a somewhat new way. But now try multiplication: “sunlight x soil = flowers” and think of the richness of what then occurs: each particle of the soil is now multiplied by the sunlight, not just the soil as a whole added to by the sunlight. Each particle of soil and each photon of sunlight interact to form something new!
THE POETIC POSSIBILITIES OF MULTIPLICATION AND LONG DIVISION
Multiplication is the best of the arithmetical procedures we learned in grade school for use in poetry because of something you might not expect of it: its richness. Consider something as simple as the poetic idea that “sunlight + soil = flowers.” Add sunlight to soil and you get flowers. (Well, you need more than that in real life, but not in poetry!) A nice enough idea that makes a pleasant poem because it expresses an old idea in a somewhat new way. But now try multiplication: “sunlight x soil = flowers” and think of the richness of what then occurs: each particle of the soil is now multiplied by the sunlight, not just the soil as a whole added to by the sunlight. Each particle of soil and each photon of sunlight interact to form something new!
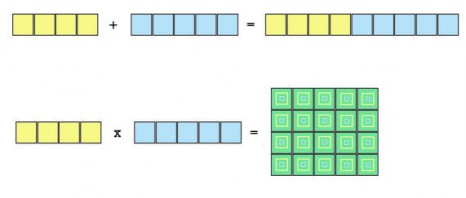
I imagine it in visual terms, addition versus multiplication:
Is not the rectangle not only a larger but a richer instance of flowers than what addition yields (even if they’re only square flowers in this case)?
And then there’s long division. As a mathematical poet, I love this procedure more than any other mathematical procedure, for look what it allows me to do with soil and sunlight:
The form allows me not only to show the effect of multiplying “soil” times” sunlight to get “flowers,” but also to show that by adding “robins” to “flowers,” I can get “spring.” The overall image is still simple but has more details than a simple multiplication could provide. And the form keeps the person engaging the poem in it longer, and the longer one is exposed to a poem, the more one should get out of it.
I imagine it in visual terms, addition versus multiplication:
Is not the rectangle not only a larger but a richer instance of flowers than what addition yields (even if they’re only square flowers in this case)?
And then there’s long division. As a mathematical poet, I love this procedure more than any other mathematical procedure, for look what it allows me to do with soil and sunlight:
The form allows me not only to show the effect of multiplying “soil” times” sunlight to get “flowers,” but also to show that “robins” added to “flowers” will result in “spring.” The overall image is still simple but has more details than a simple multiplication could provide. And the form keeps the person engaging the poem in it longer, and the longer one is exposed to a poem, the more one should get out of it.
Diary Entry for 17 November 2011, 7 P.M.: Sort of a crappy day, for me and my partner in doubles got clobbered in a league match this morning. The team as a whole won two of three, though. I actually felt pretty good on the court for a change, but made a lot of unforced errors. As for my cultural productivity, it was about the same as it has been. I got the thing above done, then used it to get this entry done. Then I worked a while on my book, finally getting the part about what I’m calling the brain’s “Anthroceptual Management Center,” or “AMC,” right, although the rightness is very badly expressed. I’m hoping to pick up speed on this section of the book tomorrow.
.