I consider myself a subauthority, third-class, concerning linguistics, but (as long-time readers of this blog will know) that hasn’t kept me from working on a theory of linguistics of my own, and frequently sounding off on the subject, as I’ve now been doing for two or three days at a thread at Aeon about an article claiming Chomsky’s theory of an innate grammar is invalid that has drawn a bunch of excellent comments, as well as many silly ones–and the usual yes or noes that airheads seem to think it worth posting to threads like this.
Hmmm, I see this is the fourth day I’ve been in and out of the thread I’m speaking of, and have already used some of what I’ve said here. I’m afraid I’m committed nonetheless to bringing you my latest comments–’cause I think parts of one or two are brilliant! Included is a post by one of the two my comments are replies to, a person using the name “Witheo.” (He’s the one I was last dealing with here.)
* * *
ME: “Just a note to indicate that I read your long reply to what I said about your linguistic nihilism, Witheo, and see that you have some goofy concept of “meaning” that I can’t deal with. Mine is simple: it is what is obviously conveyed when I show someone who speaks English a picture of an animal and ask him what it is: if it is of what I call a “cat,” then he will just about always answer, “a cat.” He and I will then have converged on the meaning of “cat” by my simple standards.
“As for Dr. Johnson, if he did not demonstrate that the rock was real, he demonstrated that it was an unreal object that had the ability to make people think it was real, and there is no difference between a real rock and a non-existent rock that human beings perceive in every possible way as a real rock.” (Note: Dr. Johnson famously kicked a rock to refute the philosopher Berkeley’s contention that nothing was real–or whatever Berkeley’s contention was–as I know most of you will have known, but perhaps not all the kids who are no doubt reading this as a fourth-grade davincianation assignment.) (Note #2: Isn’t that hilariously funny note alone worth reading this blog for a year? [Yes, I have a hydrocodone in me, with a caffeine pill. Just couldn’t get going otherwise. {Ooops–kids, don’t tell your teachers I said that! /Dang, I’m getting so inexhaustibly funny, I’ve run out of parenthetical brackets. Gotta go back to the Serious Stuff./}])
* * *
WITHEO: “How nice. That you decided to deal anyway, with my “goofy concept of meaning that you can’t deal with”. I just wish it wasn’t necessary for you to resort to ridicule everything that, by your own admission, you don’t understand. What moral advantage can you possibly hope to gain?
(Editor’s Note: When I first read the last sentence above, I thought to myself that trying for some “moral advantage” was what my opponents too-often seemed to be doing but that I almost never did; just now, though, I wondered whether or not I perhaps do try not for a moral advantage, but a sort of moral disadvantage. Why would I do that? One possibility I refuse to accept is that by coming across as a nasty fellow, I can believe opposition to my thinking is due to my opponent’s hostility to me rather than my ideas: i.e., I’m giving myself up to protect my ideas. I think a better answer, however unusual, is that I want to get my opponent to do his very best against me, fueled by RAGE. But I may be trying unconsciously to get him off-balance due to rage. Actually, my best explanation, which I’ve had for a long time, is that I truly want fully to express myself, which means expressing not only my ideas, but my feeling about those ideas, and about my opponent’s opposition–but not my opponent, because I expect an emotionally mature debater to treat the debate he’s in the same way I expect a tennis opponent to treat a match he’s in–as a fight to the death against Absolute Evil, which has nothing to do with what I think of my opponent when the debate or match is over.)
“As it happens, I would like to sincerely pretend that I can empathise, perhaps just a little, with your evident frustration. Do you feel better, when you habitually denigrate those you don’t agree with?
“You seem proud to claim that your concept of meaning is ‘simple’. I prefer to avoid that word. What may seem ‘simple’ to you (always within a certain context, specific to time and place) is not necessarily, I would venture to suggest almost certainly never, so easy to accept for another.
“You conclude, on the basis of a “simple” scenario (showing someone a picture of a cat and coming to an agreement that it is in fact a picture of a cat), that “he and I will have converged on the meaning of cat”.
“I beg to differ. What you have agreed on is that the picture is of a cat. You have not agreed, as, typically, the question did not even arise, on “the meaning of cat”. To your self-evident satisfaction, which, I hasten to acknowledge, is all that matters to us most of the time, “the meaning of cat was obviously conveyed”.
“As if ‘the meaning of cat’ could be meaningfully encapsulated in a single image. It’s not a cold silent picture that destroys our furniture and is a fussy eater and wants to be let out and then refuses to budge …
“Of course, the word ‘cat’ can be invested with numerous, often surprising, widely divergent meanings. ‘Wild cat’, ‘cool cat’, ‘alley cat’, ‘pussycat’, even an iconic brand of heavy agricultural machinery is commonly evoked as ‘a Cat’. In a court of law, the question will seem simple enough. ‘Please tell the court whether, in your expert opinion, this is a picture of the cat in question.’ (Please just say, yes or no.) Note the essential qualification. Not just any cat, but ‘the cat in question’.
“Many people like to talk about their pets. The ‘simple’ remark that ‘I have a cat’, inevitably begs the next questions, ‘what breed, male or female, how old etc.’ Suddenly, it isn’t enough that I have ‘“just a cat’.
“I guess the point I’m trying to make is that what we habitually treat as obvious ‘statements of fact’ are never the whole story. It’s the story – the narrative, if you will – that is intuitively attached to every experiential observation, that we then adopt as ‘the meaning for me’. It behooves us to keep in mind, I think, that, like it or not, each of us sees ‘the world’ differently. It’s those moccasins again, I’m afraid.”
* * *
ME: “How do you know I was replying to you with ridicule, Witheo? Haven’t you established that language can’t convey meaning. However, I agree with you that I do enjoy injecting my personal feelings into my arguments on the grounds that it will make what I’m saying more entertaining, and–I confess–because it will make me feel better by annoying someone who has annoyed me (for I have in my opinion a revenge instinct). I’m not out for moral advantage, just intellectual advantage, which I feel I always get when someone I mock makes such a big deal of it. Particularly when the mocker himself, as seems nearly always the case, has been using various kinds of mockery, such as sarcasm and superciliousness.
“To get to the meat of what I’m saying, and you would be missing if my words had meaning, is that you are saying that language has no meaning when you merely mean something very trivial: that language cannot communicate any meaning with absolute accuracy. So what? It can in all but a very few cases communicate meanings sufficiently. It really reduces to the problem of absolute truth. So far as human beings are concerned, there is no such thing–BUT there are many truths that are so far beyond reasonable doubt as to act as absolute truths, or be maximally objectively true. “Maxobjective Truths,” I call them.
“That many people–all of us at times–inappropriately perceive a text’s meaning as what we take it to be does not mean language can’t convey meaning, only that human beings can’t always use it effectively. Another dictum: any text’s meaning can require additional context to determine, as the meaning of a picture of a cat as simply “a cat” does not.
“I note you didn’t deal with what I said about Johnson.
(Editor’s Note: I’ve been defending Johnson for years, but I think my defense of him in my previous response the Witheo is as good a one as I can make.: )
* * *
ME, this time to someone named Steve Hudson, who had earlier revealed how, when he first read the article under discussion in this thread, found Chomsky’s theory be “unfounded and spurious, stupid really: “You’re sounding more sensible to me now, Steve (in merely saying the article convincingly refuted Chomsky’s but not mentioning its stupidity), but I still can’t see the article as convincingly against Chomsky rather than perhaps interestingly opposed to him. I haven’t read Chomsky myself, but what the idea of our having some sort of innate neurophysiological mechanism or set of mechanisms that greatly facilitate early language acquisition makes too much sense to me to drop on the basis of what you and others on this thread and the author of the article itself have said. Considering how important language is for us, how could we not have an innate ability very quickly to recognize a noun or a verb, tag them as such, and use them as the basis of some sort of grammar that helps us pick up language?
“Common sense also tells me that we instinctively can tell human speech from other sounds, including (most) sounds animals make, except cats, although they mostly keep their supra-human intelligence to themselves.”
* * *
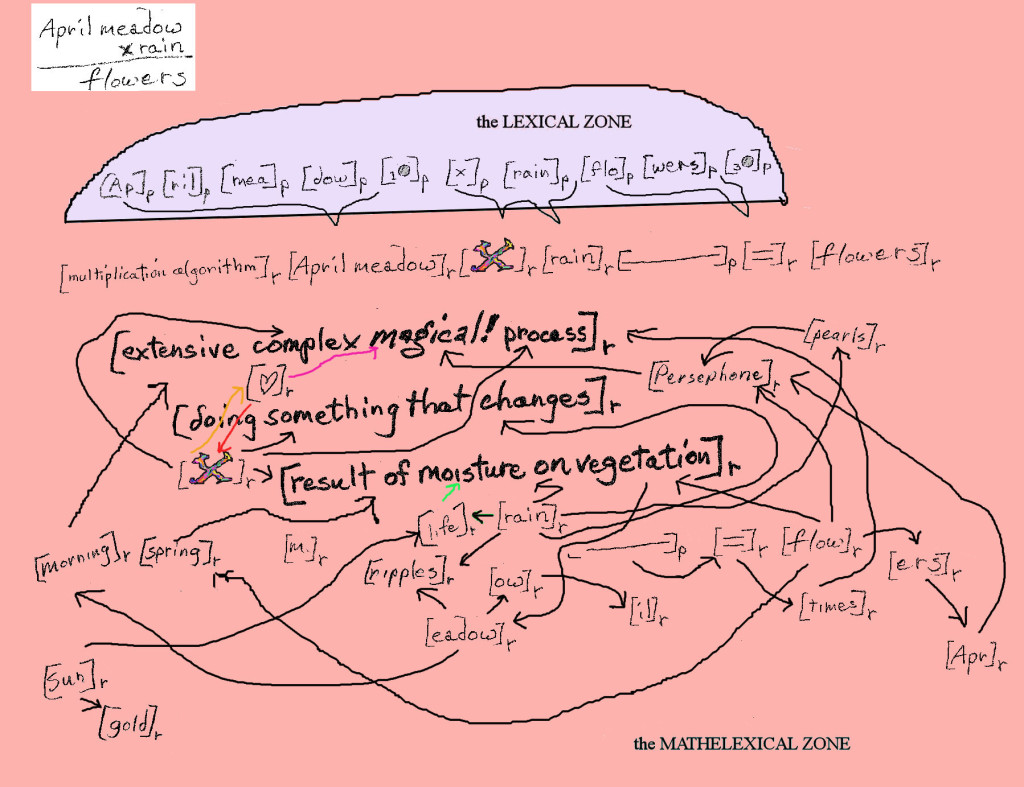
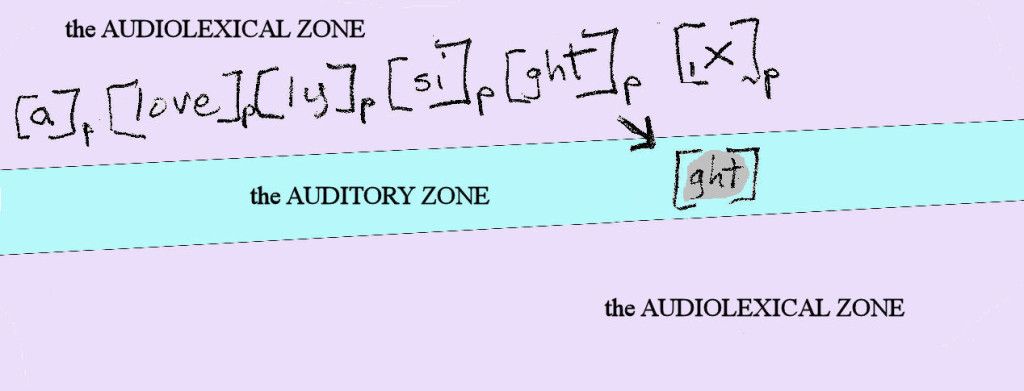
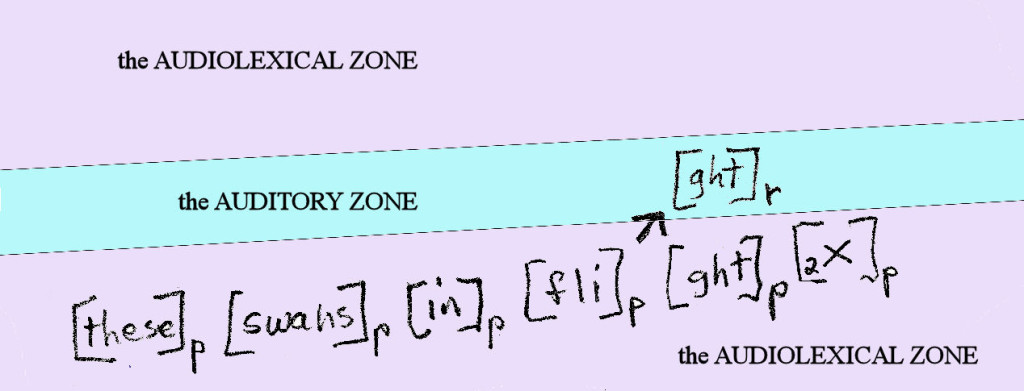
My theory, I think, is a clumsy mess so far, with gaps I have no idea yet how to remove, but it’s fun for me to work on it, and I think I’ve said one or two interesting things in it. So I’m afraid I’ll keep talking about linguistics here as long as I continue blogging.
.