Notes on Bob Grumman’s Mathemaku
and on
Mathematical Poetry Generally (*)
with additional commentary by John Randall, Associate Professor of Math at Rutgers University |

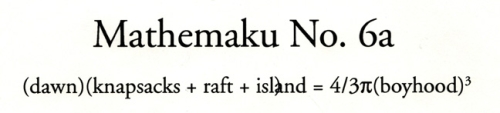
“One cannot step twice into the same river, for the water into which you first stepped has flowed on.”
–Herakleitos, 21, trans. by Guy Davenport
“Discourse is like a river.”
–Gregory Vincent St. Thomasino
“If to the moment I should say: Abide, you are so fair.”
–Goethe. Faust.
The point I wish to make is two-fold: It is (1) that the mathematical symbols employed by the poet are not merely typographically convenient; that is to say, they are not ornamental, they are not adventitious –and so cannot be dispensed with if the poem is to be the poem that the poet intends it to be. And (2) that the poet is doing what poets have always set out to do; namely, to give permanence to the transitory, to make permanent the transitory, or fleeting, poetic intuition. But that this poet presents us with a most signature strategy toward that end.
The first particular to note about the mathemaku (and about mathematical poetry, generally), is that it is not about mathematics per se. This point is fast set forth, along with some terse historical account as to mathematical poetry’s possibleantecedents, by Bob Grumman in his essay, “Of Segreceptuality and Mathematical Poetry.” (1) There Grumman writes, “Of course, mathematics has for a long time occasionally gotten into poetry, but until this century only as subject, not as actual component. In other words, there had been poems about mathematics (by some of the 17th Century metaphysical poets, for example), but no poems that were mathematics.” (2)
Furthermore, it is important to note that the mathemaku is not heuristic, there is no logic of discovery going on–save for what the reader “discovers” on his own as he reads or scans the poem. (This process of reading, or discovery, this processing of information, I call–according to the program, logoclastics– redding [generally, redding is the putting into order ].)
Inasmuch as the poetic intuition is presented to us in this mathematical language, this nonlinguistic symbolic system!, themathemaku is after the fact; the poetic intuition has already been formed (it has already been articulated), and what we are presented with is a transliteration –the result, the object, of a giving over of one language, or of one order of language (theto express in words ), for another (the to express in mathematical symbols, a mathematical nomenclature–and thismathematical nomenclature has not been cynically appropriated, it is not a mere associative reinforcement, but rather is it the embodiment of the poem–it is the vessel through which the poem is conveyed, it is its concrete expression). The transliteration is, from a language into a notation; from words, into a nonlinguistic system of signs representative of words.
In the mathemaku we are presented with nothing of the pre-history of the poetic intuition, we have nothing of its adventure, of its struggle into being and which, I would contend, can only be portrayed in words, and not in a form–the mathemaku form–that is as such twice removed. For in the redding of the mathemaku, we are redding from mathematical symbols backinto words, we are interpreting, denoting, these / each mathematical symbols into groups of words, and then articulating these discrete, that’s not to say unconnected, groups together into one at last paradepictive paragraph. (But this pre-history of the poetic intuition, it is not present in the haiku either. . .).
For finally it is by way of words that the poetic intuition, the poetry, is grasped by the understanding of the reader; again, we are reading from a mathematical nomenclature, back into the colloquial language of poetry, or a paraphrase of that poetry, which nonetheless involves us again with an ambiguous and inexact, if not indeterminate, language; (3) what we are presented with, is the poetic intuition concretized; it is the poetic intuition given definite form, and for all time; it is the poetic intuition preserved, presented as a permanent and unchanging truth, now and forever (or else so long as the symbols of mathematics continue to indicate what they indicate, and are not changed or modified in what they signify, in their denotation, e.g., so long as the mathematician’s k [or c, C, or K] stands for a mathematician’s constant). (What is the relationship between the mathematician’s constant and the constant of colloquial language? In Grumman’s usage, does the meaning not fluctuate between the one and the other? In the redding, are we not taking the one for the other?)
Grumman has so composed his poem that there is, on the one hand, little room for ambiguity (so far as these mathematical symbols stand alone as mathematical symbols), but then on the other hand, while I would not say this ambiguity is to instance the instability of meaning, we might take it to be the ambiguousness of poetic language generally. (We must bear in mind that the word ambiguous means having several possible meanings or interpretations. ) If we look at what are his strictly mathematical symbols–as distinct from what are musical notations (these appoggiaturas or grace notes ), and then the one astronomical symbol standing for the sun –beginning with the symbol 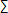 , sigma, which of course stands for sum, or,the summation of, and has a sense similar to that of the symbol , sigma, which of course stands for sum, or,the summation of, and has a sense similar to that of the symbol 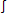 (the mark that looks like the letter s, an s which stands for summation), which stands for integral, and indicating that the expression following it is to be integrated, and then the symbol k, which as we noted stands for constant, and then of course the symbol +, which is the plus sign, the sign of in-addition-to, and also the sign for positive, we can see that his “mathematical expression” is the transliteration of a thought, an idea-about. This idea–and, ideas are, properly speaking, or so I would contend, always about something –is the poetic intuition–and, a poetic intuition is always an epitome. (the mark that looks like the letter s, an s which stands for summation), which stands for integral, and indicating that the expression following it is to be integrated, and then the symbol k, which as we noted stands for constant, and then of course the symbol +, which is the plus sign, the sign of in-addition-to, and also the sign for positive, we can see that his “mathematical expression” is the transliteration of a thought, an idea-about. This idea–and, ideas are, properly speaking, or so I would contend, always about something –is the poetic intuition–and, a poetic intuition is always an epitome.
I want to say immediately, that what is going on in the mathemaku is not a quantification, a measurement, of emotion (something that has been tried by the psychologists and shown to be, at last, unreliable). The implications of this giving over of one language, or order, for another are far greater than any scientific or systematic quantification of the emotions (which in the final analysis is more to do with and about neuronic transmissions and changes in pulse rate and breathing, more to do with the autonomic and central nervous systems, than with what we would term, if poetically, and according to common sense, an emotion ).
We have to ask, why has it become necessary for the poet to change over to mathematical symbols, to the nomenclature of mathematics, in order to achieve this permanence and immutability, has he not available to express in words in order to achieve this aim, this aim that is it not the end of all poetry to make permanent the transitory?
Indeed, Grumman allows of such a question in his essay. “If the point of the poem,” he asks, “could be conveyed in words, why complicate things with mathematics?” He answers that, appreciating an artwork from more than one major part of the brain at once is more pleasurable than appreciating it segreceptually, i.e., rather than in one perceptual or conceptual area of the brain at a time; and, but what is of more interest to us here in these notes, that the mathematics not only speaks to the ultimate oneness of all forms of human creativity, but that it illustrates the gradations of speech that the poem is about, and serves to maximize their –the gradations of speech, that is– concreteness. We must point out, that nowhere in his brief essay does Grumman provide the architecture to support his insight that the brain does function in this way, and we are reminded of Pound’s logopoeia, but be that as it may, he does have a fertile metaphor, and his point is not lost. (And we would be remiss if we did not acknowledge the now vast literature that exists on the subject of the brain and its functions, specificallycognition, much of which makes up the very architecture pertinent to Grumman’s point. But still, even if we take him on his word, even if we can accept, however provisionally, that a poem in mathematical notation speaks to the ultimate oneness of all forms of human creativity (and what is so special about the nomenclature of mathematics that it can do this; is it because its indices are constant; is it because mathematics is a universal language; or, what’s more intriguing still, has the poet found in the mathematiucal nomenclature a new voice of “negative capability”; has he found that our problematics are the “uncertainties, Mysteries, doubts, without any irritable reaching after fact & reason” of a language whose stability of meaning is obliterate?), it is a glaring leap to leave unaddressed the question whether, apart from the visual cortex–the information processing system at which awareness makes its most passive grasp at an object and template recognition occurs–the brain does in fact use a different area to know at mathematical symbols than it does to translate those symbols into words–isn’t it all but a matter of memory, and context and expectations? This question goes to the heart of the matter, and informs that of the general aesthetic appreciation of the artwork. It is often the case in the writings of Mr. Grumman, that he takes for granted our knowledge of the fields not only of modern and classical literature, but of psychology and philosophy as well. A consequence of this is that his writings must be elaborated on by other writers.) We ought as well to say, that nor does he mention anything at all to do with the making permanent of the transitory, which is the reading / interpretation driving these notes. Does the mathemaku resist my reading?
From the perspective of logoclastics, we might answer that, because words have been shown to undergo modifications, qualifications and limitations, if not outright changes, to their meanings. Indeed, some words become archaic, because their usage has become rare; and some words become obsolete, because they have been replaced by other words, or phrases, which better serve their purpose of indication. A simple formula to follow, in understanding these modifications to words, would be, that since every use of a term in a new context gives it a new meaning, there are as many meanings as there are contexts. So far as this goes, this is pretty sound policy, and we need only pick up an unannotated edition of Shakespeare to gain a first hand experience of archaisms and obsolete words, that is of the time it takes to track down their modern equivalents. (4)
But this is really only one side of the situation, it has now entered abruptly upon the poet that he is living in what may arguably be described as a post-logocentric climate. The poet learns that his discourse (that poetic intuition, that poetic insight, to-be-conveyed to his reader, or else, to be immortalized, and but of course the structure of language whose aim it is to carry this out), the poet learns that his discourse, once held to be centered in his words, and kept safe by the stability of the meaning of those words, has been cut adrift, has all but poof evaporated, is ob-literate, strictly expunged from the letter; he learns that his discourse has no center, as such, but that it has innumerable centers . . . innumerable configurations . . . as great as is the future times to come, so great in number are the contexts and expectations he must preface! This is not but a matter of his future readers finding their modern equivalents, nor is it a matter of their understanding his poem according to the meanings of the words at the time during which he composed it (that is, moreover, their taking into account of the poet’s social, historical and psychological contexts, a matter of syntax and context); it is . . . a matter of his contemporariesunderstanding the poem to be the poem that he intends it to be.
It is not too great a reach to compare this situation, this state of affairs, to when in ancient and mediaeval times almost all scholars believed that the Earth was situated, really affixed, to the center of the universe; that the Earth was truly motionless, in a state of absolute rest; and all motion could then be measured relative to such a point–being the Earth–at absolute rest, and we would then have an absolute motion upon which all observers could agree. Any observed motion that was not equivalent to the absolute motion, was the result of the absolute motion of the observer. And then, in the year 1543, there appeared De Revolutionibus Orbium Coelestium Libri IV by Nicolas Copernicus, in which was put forward a heliocentric theory of the universe; and then in 1781, Immanuel Kant published the first edition of his Critique of Pure Reason, which included the famous passages on the transcendental deduction of the categories, and in which he (in the preface to the second edition, 1787) compares his answer to the question, How is synthetic a priori knowledge possible?(that answer is, of course, to do with what he termed, “transcendental idealism” ) to the Copernican revolution in astronomy; and now, today, we are undergoing the incidental effects, the fallout, perhaps, of a third “Copernican revolution,” an intellectual revolution that is still shaking ground, and that will continue to shake ground, and beyond the reams of literature and literary criticism, to architecture, and to music, and even to mathematics. (Whereas with Copernicus, man had lost his privileged position in the universe, today we are bearing witness as signification loses its privileged position in discourse.)
The poet John M. Bennett has been kind enough to consider my assertions here, and he remarks that this transliteration may be, if not an out-and-out making permanent of the transitory, than at least an attempt at “slowing down.”
And one might construe this “slowing down” to refer to the process (a slowing down of this process) by which things once thought permanent are revealed to be in fact not permanent at all but transitory. In this sense, then, this slowing down would be a sort of mechanical metaphor, pointing to the overall significance of the mathemaku.
On the other hand, one might just as well construe this “slowing down” to refer to the “discovery” process of the reader; a slowing down of the reading so as to allow the reader the occasion or opportunity for re-consideration.
In both cases, however, what is being slowed down is indeed the reader’s activity, his redding. But since it is what the reader brings to the text (by way of his very own contexts and expectations) that determines, ultimately, the meaning of the text, this strategy would seem ineffective, ineffective to make permanent the transitory (unless we were willing to happy ourselves with a metaphor, which in the long run may be all– ought it to be all? –we can to a reasonable degree expect from a poem . . . ).
To what end or purpose, then, this “slowing down”?
In either case, this slowing down is with reference to time . It is a deliberate manipulation of the time, not in the sense of metre, but of the time of the reading process, in the sense of to slow down the reading . Perhaps we can say that this manipulation of time is in itself a metaphor for. . . .
Let us consider this quote from Paul Valéry: “The symbol is to some extent a time machine. It is an inconceivable shortening of the duration of mental operations, to the point where one might almost define the world of mind as the world in which one can use symbols.” (5)
Perhaps we can say that this slowing down, this manipulation of time, in a mechanical sense, is a metaphor for the operations of the mind when to do with symbols, and however obtuse, however imprecise it may be, the poet, by composing his poem so as to admit of this slowing down, is by way of this slowing down creating a metaphor, and by way of this metaphor making reference to the operations of the mind when to do with symbols. Is this Grumman’s answer to segreceptuality . . . ? Is this another note in the philosophy we know of as of-manywhere-at-once…? What better instance of such, than of the symbol. . . .
But then again, why not, this “slowing down,” to be a strategy for inducing in the reader, the experience of to-defer…?
Still, granting all that, would it not be nonetheless as artificial, as man-made, a contrivance as the illusion of permanence or stability of meaning that has been shown to attend our discourse for the last two thousand years…?
It is my assertion, that this transliteration, while although it may be a “slowing down” in some or other specific sense–it is my assertion that this transliteration, this giving over of one language or order for another, is the poet’s attempt, but as though he can do none other, to give permanence to the transitory, and that given the awareness of the mostwise arbitrary, and ever changing meanings of words, he has turned to mathematical symbols, to a mathematical nomenclature, as a source of reliable and dependable meanings, as an ever-increasing set of eternal, immutable truths, for to achieve this / his end. (But are mathematical symbols indeed “dependable”?
At this point, certain questions are raised, and no less than to the immutability, to the infallibility or permanence of mathematics and its symbols; the articulation of these questions, and their discussion, is, happily, beyond the scope of these notes; I have, above, at least hinted at one such controversy, that ultimately we are turned back to words if we are to grasp at the poetry contained in the mathemaku, for the mathemaku is in ways a container, a hermetically sealed chamber or vault–the poem is given to a mode of existence, being the mathematical syntax or sentence or formula or proposition–in name if not in fact, in word if not in object, keeping safe its contents but as though to foreclose or exclude successive horizons of expectations, keeping safe its contents from the encroachments of new contexts, new meanings, nay, a revolution in how things are thought. . . .
And yet on the other hand, it may increase us to consider that, the poet has not stood still and accepted his fate, or at least that fate that has at last caught up with letters; the poet has moved on, in his attempt to give permanence to the transitory; in this case he has moved on to mathematical symbols, to the nomenclature of the mathematician; and this may very well mean that the will to give permanence to the transitory ( Moment, abide! ), like faith in the transcendent, and like the poetic insight itself, is something that can only be lost, but that it cannot be erased. . . .
Commentary by John Randall, Associate Professor of Math at Rutgers University
The symbols of mathematics are by no means permanent. Probably the most enduring are the “Arabic” numerals, which have been around for about 1000 years. Everything else is much more recent.
Literal symbols for unknowns were introduced by the Italian algebraist Vieta (1540-1603), who still used aequare to denote equality. (6)
Our modern sign for equality was introduced by Robert Recorde, the English Royal Physician, in 1557. (7)
Signs such as 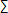 (for summation) and (for summation) and 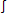 (for integration) were introduced much later, moreover, their meaning has changed. The meaning of infinite sums was not sorted out until the 19th century. Misunderstandings of the nature of convergence caused luminaries such as Cauchy to misstep. Our modern usage of the integral sign (for Riemann-Stieljes integration) dates to the early 20th century. While integration of simple functions would have been written in a similar way by the 18th-century mathematicians, their notation of function (as a particular kind of relation given by a formula) is far less general than ours. (for integration) were introduced much later, moreover, their meaning has changed. The meaning of infinite sums was not sorted out until the 19th century. Misunderstandings of the nature of convergence caused luminaries such as Cauchy to misstep. Our modern usage of the integral sign (for Riemann-Stieljes integration) dates to the early 20th century. While integration of simple functions would have been written in a similar way by the 18th-century mathematicians, their notation of function (as a particular kind of relation given by a formula) is far less general than ours.
While mathematicians have been agreed on the meaning of the positive integers for several hundred years, even the negative integers were regarded as mere artifice until more recently. A precise definition of the real numbers was given little more than 100 years ago by Dedekind. Notation is even more transient: Newton’s mathematical work is now readable only by specialists, not by mathematicians.
To assume that through mathematical and musical ideas and notation one can transcend time seems to ignore history. Both depend on their culture and time, just as language does.
The transcendent intent of the mathemaku is perhaps better construed as allegory rather than actuality. The inclusion of flawed technical notations assumed to be unfamiliar to the reader is at best mysticism and at worst mere appropriation.
A Note on Randall, by Gregory Vincent St. Thomasino
In regard to the use of aequare (which is Latin for to make equal ) to denote equality, and in keeping with the context ofletters, my instincts turn me to Shakespeare, who wrote in his Romeo and Juliet, “What’s in a name? That which we call a rose by any other name would smell as sweet.” And with an invocation to Gertrude Stein, from her poem, Sacred Emily : A rose is a rose is a rose is a rose. The point is this: Whether I am writing the word “constant,” or the symbol, the notation, “k,” my responsibility, to the poem, is to make accessible to my reader (that is, to make my reader open to the influence of) the idea of unchangeableness or without vary . If I am writing in the traditional haiku idiom, I might use the word “constant,” and if I am writing in the mathemaku idiom, I might use the symbol “k.” In both equations, the idea of unchangeableness is stable ( stable, that is–and pardon, please, if I am in effect treating an abstraction as though it were substantially existing, if I am, that is, reifying–to the extent whereas this thing I call a rose will smell just as sweet regardless of whether I call it “rose” or “rosa,” or “rhodon”), but to the degree that its sense is turned by my use of it in the poetic context–the idea of unchangeableness in and of itself is an abstraction, there must be an unchangeableness with regard to something. The changes we are concerned with here are not the changes to name, but to meanings, indeed to what the names are pointing to. In other words, the sign may change, indeed the mark may change from a word to a symbol, but what matters to us most is (1) its link by social convention to (2) what it stands for. (Robert Recorde’s use of the twin lines as a mnemonic–i.e., assisting the memory–shorthand for equals stuck, and continues to stay, because it works better than writing the wordaequare. Here, the authoritarianism, or, power, or, mental force, is sheer practicality!)
And if you’ll grant me that the mathemaku is a work of logoclastics , then to consider its success–with regard to its transcendent intent, but then as a work of art on the whole, if you will–in terms of allegory (Edward Gorey?), rather than in terms of actuality, only, methinks, increases it by lending to it a certain concept of . . . but irony is a word I am no longer taken with, today I can think only in terms of whimsicality. Even wistful, characterized by pensive longing. . . . Ah, that is the dominant seventh!
Notes:
(*) A version of this article first appeared in Meat Epoch #20, March 1997.
(1)Central Park, (Spring number, 1994).
(2) In his poem “The Phoenix and the Turtle,” Shakespeare makes reference to number and mathematics as being useless to in any positive sense describe or measure the high chaste love that did hold between the birds. And it is important to bear in mind, and no less in the context of Grumman, that the Phoenix is the symbol of love and the Turtle Dove of constancy. Grumman’s use of mathematics is most always to the positive sense. He writes, “I’m no authority on the subject but my impression is that the first true mathematical poem occurred in Louis Zukofsky’s A, which was published in 1969. Whatever the truth of the matter, that was myintroduction to the form, . . .” It is interesting that Grumman does not cite Paul Valéry (if not for an actual occurrence of the mathematical poem, then perhaps as a precursor, or at least for moral support) who had a strong attraction to mathematics. Valéry wrote in his Notebooks that he wanted “to amuse myself by translating everything into mathematics.” (See the commentary by John Randall, especially his valuable suggestion that the mathemaku be read as allegory.)
(3) And while one can argue that all works are to good extent “indeterminate,” and that some works are deliberately explorations of indeterminacy, as most works of logoclastics are, I say–and rest these notes upon this–that that is not the case with the mathemaku. Rather, much to the contrary. . . . The mathemaku is not a deliberate exploration of indeterminacy, but is a strategy after permanence of meaning. (I wonder at the optimism of this strategy, as I consider all works of logoclastics at basis a response to the dystopic. In this case, the poet’s foreclosure is with regard to change; his promise for his poem is not so much a stasis or still life or time-capsule effect; rather, a utopia. No matter that this utopia is hypothetical.
The range of the works of logoclastics is vast, and includes the whole of Language writing, and includes not only those works that are deliberately explorations of indeterminacy, in themselves and in the redding, but all works that present us with a break or dislocation of discourse, all works that in effect induce a collaboration in the creation of meaning, all works that induce a narrativity in the reader. For starters, all works that begin in the consciousness that ours is a post-logocentric climate, all works that begin in the consciousness that discouse is no longer centered in words but occurs in the text’s being redd– these are works of logoclastics! )
(4) For a wonderful elaboration of this “problem,” and on the art of reading generally, see Jorge Luis Borges’ short story, “Pierre Menard, Author of the Quixote,” collected in Labyrinths
(5) Quoted in Roger Shattuck, The Banquet Years , p., 242.
(6) That is to say, Vieta actually wrote the word aequare to indicate that the terms separated are equal where we would use the symbol of the two parallel lines, =, to indicate such. Vieta did not have at his ready the modern equals sign; it was not invented yet or else he was unaware of its coming into use!
(7) Note how the symbol (the mark ) resembles its meaning! Recorde wrote, in his textbook of algebra entitled The Whetstone of Witte, “I will set as I do often in work use, a pair of parallels, of twin lines of one length, thus: =, because no two things can be more equal.” |